
Rocketdyne F-1 rocket engine used by Saturn V S-1C first stage
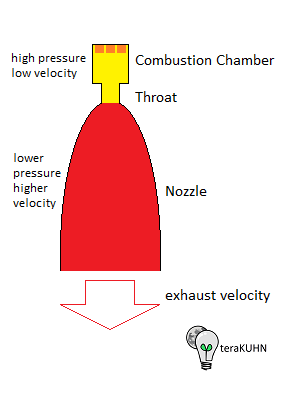
Rocket engine combustion chamber, throat, nozzle, and exhaust
Rocket Science or Aerospace Engineering is the engineering field that covers the development of spacecraft.
This page is intended to provide formulas and pointers to software that can help with rocketry. The software referenced here is all either free, inexpensive, or demo software so it can be tried without initially investing significant money. Where possible we've included a link to the site where you can get the latest version rather than a direct download of a possibly stale version.
If you want to learn about rocketry, check out
As mentioned in other pages on this web site, launch systems typically use chemical rockets. Rockets use fuels that go through a chemical reaction to release energy. This released energy heats the exhaust gas creating a lot of pressure in the rocket engine combustion chamger. This pressurized gas is guided by the rocket engine nozzle into a high-speed exhaust stream which produces thrust. Alternatively, rockets can use electric charge to accelerate particles into a high-speed exhaust stream which causes the spacecraft to accelerate in the opposite direction. On Earth (or other planets), the force of this thrust works against the force of gravity which pulls a rocket towards the surface of Earth (or other planets). Once a rocket is moving through the atmosphere, there's also a force of drag on the rocket. Thus the acceleration of a rocket depends on multiple forces acting on it, which includes:
rocket thrust:
- a = Ft / m
where:
- Ft is the force of the rocket thrust, and
- m is the mass of the rocket
drag:
- a = ( Cd * p * A * v^2 / 2 ) / m
where:
- Cd is drag coefficient,
- p is the density of the atmosphere,
- A is the cross sectional area,
- v is the velocity, and
- m is the mass of the rocket
gravity (of Earth near the surface):
- a = 9.8
Also, noted on other pages on this web site, launch systems typically use chemical rockets to accelerate spacecraft to Earth orbit or farther. Rockets use fuels that go through a chemical reaction to release energy. This released energy heats the exhaust gas creating a lot of pressure in the rocket engine combustion chamger. This pressurized gas is guided by the rocket engine nozzle into a high-speed exhaust stream which causes the rocket acceleration. Some common rocket fuels are:
- liquid propellants
- Liquid hydrogen and liquid oxygen (LH2/LOX) 2(H2) + O2 -> heat + 2(H2O)
- Kerosene and liquid oxygen (RP-1/LOX)
- Unsymmetrical dimethylhydrazine and dinitrogen tetroxide (UDMH/N2O4) N2C6H8 + N2O4
- Aerozine/dinitrogen tetroxide (A-50/N2O4)
- Ammonium perchlorate composite solid propellants (APCP)
- aluminium and ammonium perchlorate Al + NH4ClO4
- magnesium and ammonium perchlorate Mg + NH4ClO4
- zinc and ammonium perchlorate Zn + NH4ClO4
- Hydroxyl-terminated polybutadiene (HTPB) and ammonium perchlorate
- Polybutadiene acrylonitrile (PBAN) and ammonium perchlorate
In addition to liquid propellant chemical rockets and solid propellant chemical rockets, once off the Earth's surface, spacecraft can use electric propulsion (aka ion thrusters) or solar sails (aka light sails). In the case of ion thrusters, instead of heated gas creating pressure that is guided into a high-speed exhaust stream they use electric charge to accelerate particles into a high-speed exhaust stream which causes the spacecraft to accelerate in the opposite direction. In the case of solar sails, photons of light, typically from the Sun, are reflected causing acceleration in the opposite direction.
Except for solar sails, all of these propulsion mechanisms follow the basic principle of a rocket which is to accelerate itself by creating thrust by expelling part of the rocket vehicles original mass, typically the fuel and oxidizer, at high velocity. A solar sail works by reflecting photons of light which are not part of the sail vehicles original mass. The rocket equation (aka Tsiolkovsky rocket equation, classical rocket equation, or ideal rocket equation) describes the motion of vehicles that follow the basic principle of a rocket:
- delta-v = ve * ln ( m0 / mf ) = Isp * gn * ln ( m0 / mf )
where:
- delta-v is the change in velocity of rocket vehicle
- ve is the average velocity of the rocket exhaust
- ln is the natural logarithm function
- m0 is the initial total mass, the rocket and fuel mass or wet mass
- mf is the final total mass after exhaust, the rocket without fuel mass or dry mass
- Isp is the specific impulse
- gn is the acceleration due to gravity
As the specific impluse of the rocket increases so does the delta-v that can be applied to the rocket vehicle. Also note that as average exhaust velocity increases so does the specific impluse of the rocket:
- Isp = ve / gn
where:
- Isp is the specific impulse
- ve is the average velocity of the rocket exhaust
- gn is the acceleration due to gravity
Note that unlike rocket propulsion systems, solar sails do not create thrust by ejecting part of the crafts mass as rocket fuel and oxidizer. Solar sails utilize the solar wind of photons to provide a momentum change to propel a craft through space. They work by reflecting photons of light which are not part of the solar sail craft original mass. A solar sail may be effective anywhere where the solar wind is present and there is so little atmosphere that the sail doesn't create significant drag. Solar sails use an ultrathin membrane that is deployed in space to form a sail. The sail is controlled and maneuvered so that it is able to use the direction of the solar wind to sail through space, guiding itself much like a sailboat changes trajectory by altering the position of the sail against the wind. In Earth orbit, depending on the sail design, sail force and atmospheric drag force would be equal at an altitude of between 500 and 1000 km, which means that a solar sail craft would have to deploy above this altitude.
| Technology | thrust range | specific impulse range (s) | type |
|---|---|---|---|
| Hydrazine Monoprpellant | 0.25 – 25 N | 200 – 285 | Chemical |
| Alternative Mono- and Bi-propellants | 10 mN – 120 N | 160 – 310 | Chemical |
| Hybrids | 1 – 230 N | 215 – 300 | Chemical |
| Cold / Warm Gas | 10 μN – 3 N | 30 – 110 | Chemical |
| Solid Motors | 0.3 – 260 N | 180 – 280 | Chemical |
| Electrothermal | 0.5 – 100 mN | 50 – 185 | Electric |
| Electrosprays | 10 μN – 1 mN | 225 – 5,000 | Electric |
| Gridded Ion | 0.1 – 20 mN | 1,000 – 3,500 | Electric |
| Hall-Effect | 1 – 60 mN | 800 – 1,950 | Electric |
| Pulsed Plasma and Vacuum Arc Thrusters | 1 – 600 μN | 500 – 2,400 | Electric |
| Ambipolar | 0.25 – 10 mN | 400 – 1,400 | Electric |
| Solar Sails | TBD | NA | Propellantless |
| Electrodynamic Tethers | TBD | NA | Propellantless |
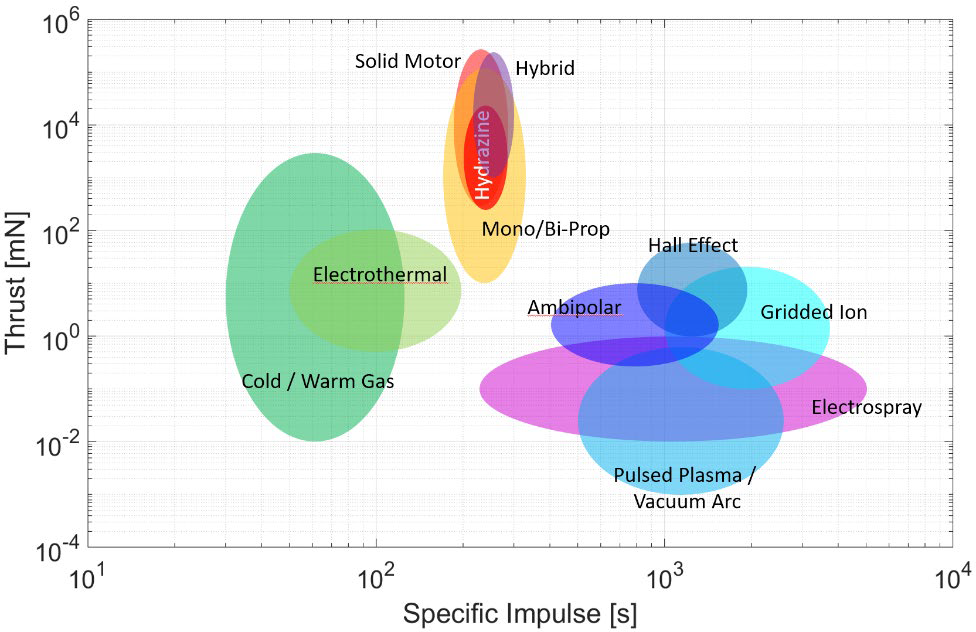
CubeSat in-space rocket propulsion systems (thrust vs. specific impulse). Credit: NASA
Understanding the characteristics of a rocket can be used when designing launch systems and landing systems. As an example, imagine that you start with a 6U CubeSat heading directly for the Moon. In order to slow down and do a soft landing you need to decrease the crafts velocity relative to the Moon from about 2.6 km/s to zero. While most model rocket engines have specific impulses between 50 and 100 seconds, commercial solid rocket engines have specific impulses between 200 and 280 seconds. Thus solid rocket motors can have an exhaust velocity around 2,600 m/s, although this depends on the fuel, oxidizers, and rocket nozzle used. By aiming the rocket motor in the right direction, the velocity relative to the Moon could be eliminated, while consuming some of the mass of the craft as fuel and oxidizer. A 6U CubeSat can have a mass of about 12 kg. Using the above equation for delta-v we get:
- delta-v = ve * ln ( m0 / mf ) = Isp * gn * ln ( m0 / mf )
- 2,600 m/s = 2,600 m/s * ln ( 12 kg / 4.4 kg )
With the craft having a final mass of 4.4 kg, about 7.6 kg have been used up as fuel and oxidizer ejected by the rocket engine. In addition to the 7.6 kg of mass used as rocket fuel and oxidizer, since rocket motors structure has some mass also, we can expect to use up at least 9.6 kg. This leaves you with about a 2.4 kg lander, drastically smaller than most landing systems flown. For reference, the OMOTENASHI cubesat's surface probe's mass is just 0.7 kg.
